Example 2 - 3D: Simple 3D cell signaling model

Example 2 - 3D: Simple 3D cell signaling model#

We model a reaction between the cell interior and cell membrane within a dendritic spine:

Cyto - 3D spine volume
PM - 2D cell boundary

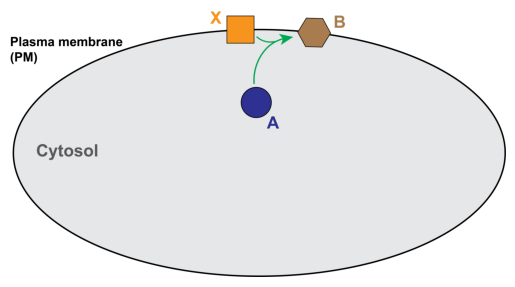
Model from Rangamani et al, 2013, Cell. A cytosolic species, “A”, reacts with a species on the PM, “B”, to form a new species on the PM, “X”.

\[\begin{split} \frac{\partial{C_A}}{\partial{t}} = D_A \nabla ^2 C_A \quad \text{in} \; \Omega_{Cyto}\\ \text{B.C. on A:} \quad D_A (\textbf{n} \cdot \nabla C_A) = -k_{on} C_A N_X + k_{off} N_B \quad \text{on} \; \Gamma_{PM} \end{split}\]

Similarly, the PDEs for X and B are given by: $$ \frac{\partial{N_X}}{\partial{t}} = D_X \nabla ^2 N_X - k_{on} C_A N_X + k_{off} N_B \quad \text{on} \; \Gamma_{PM}\\ \frac{\partial{N_B}}{\partial{t}} = D_B \nabla ^2 N_B + k_{on} C_A N_X - k_{off} N_B \quad \text{on} \; \Gamma_{PM} $$

import matplotlib.image as mpimg
from matplotlib import pyplot as plt

img_A = mpimg.imread('axb-diagram.png')
plt.imshow(img_A)
plt.axis('off')

(-0.5, 5830.5, 3140.5, -0.5)

../../_images/9bce0baf037e972455d12e0677928855de003516bac8b8befb60cf04ce0ad4ff.png

Imports and logger initialization:

import logging
import pathlib

import dolfin as d
import numpy as np

from smart import config, mesh, mesh_tools, model, visualization
from smart.model_assembly import (Compartment, CompartmentContainer, Parameter,
                                  ParameterContainer, Reaction,
                                  ReactionContainer, Species, SpeciesContainer)
from smart.units import unit

logger = logging.getLogger("smart")
logger.setLevel(logging.INFO)

/usr/lib/python3/dist-packages/scipy/__init__.py:146: UserWarning: A NumPy version >=1.17.3 and <1.25.0 is required for this version of SciPy (detected version 1.26.4
  warnings.warn(f"A NumPy version >={np_minversion} and <{np_maxversion}"

First, we define the various units for use in the model.

um = unit.um
molecule = unit.molecule
sec = unit.sec
dimensionless = unit.dimensionless
D_unit = um**2 / sec
vol_unit = unit.uM
flux_unit = molecule / (um**2 * sec)
surf_unit = molecule / um**2

Next we generate the model by assembling the compartment, species, parameter, and reaction containers (see Example 1 for or API documentation for more details).

# =============================================================================================
# Compartments
# =============================================================================================
# name, topological dimensionality, length scale units, marker value
Cyto = Compartment("Cyto", 3, um, 1)
PM = Compartment("PM", 2, um, 10)
cc = CompartmentContainer()
cc.add([Cyto, PM])

# =============================================================================================
# Species
# =============================================================================================
# name, initial concentration, concentration units, diffusion, diffusion units, compartment
A = Species("A", 1.0, vol_unit, 1.0, D_unit, "Cyto")
X = Species("X", 1000, surf_unit, 0.1, D_unit, "PM")
B = Species("B", 0.0, surf_unit, 0.01, D_unit, "PM")
sc = SpeciesContainer()
sc.add([A, X, B])

# =============================================================================================
# Parameters and Reactions
# =============================================================================================

# Reaction of A and X to make B (Cyto-PM reaction)
kon = Parameter("kon", 1.0, 1/(vol_unit*sec))
koff = Parameter("koff", 0.1, 1/sec)
r1 = Reaction("r1", ["A", "X"], ["B"],
              param_map={"on": "kon", "off": "koff"},
              species_map={"A": "A", "X": "X", "B": "B"})

pc = ParameterContainer()
pc.add([kon, koff])
rc = ReactionContainer()
rc.add([r1])

Now we load in the dendritic spine mesh and generate the marker functions mf3 and mf2.

# Load mesh
spine_mesh = d.Mesh('spine_mesh.xml')
mf3 = d.MeshFunction("size_t", spine_mesh, 3, 1)
mf2 = d.MeshFunction("size_t", spine_mesh, 2, spine_mesh.domains())
visualization.plot_dolfin_mesh(spine_mesh, mf3, clip_origin=(0.143, 0.107, -0.065))

ROOT -2024-07-21 19:14:38,295 trame_server.utils.namespace - INFO - Translator(prefix=None) (namespace.py:62)

ROOT -2024-07-21 19:14:38,332 wslink.backends.aiohttp - INFO - awaiting runner setup (__init__.py:122)

ROOT -2024-07-21 19:14:38,333 wslink.backends.aiohttp - INFO - awaiting site startup (__init__.py:129)

ROOT -2024-07-21 19:14:38,334 wslink.backends.aiohttp - INFO - Print WSLINK_READY_MSG (__init__.py:135)

ROOT -2024-07-21 19:14:38,335 wslink.backends.aiohttp - INFO - Schedule auto shutdown with timout 0 (__init__.py:143)

ROOT -2024-07-21 19:14:38,336 wslink.backends.aiohttp - INFO - awaiting running future (__init__.py:146)

Write mesh and meshfunctions to file, then create mesh.ParentMesh object.

mesh_folder = pathlib.Path("spine_mesh")
mesh_folder.mkdir(exist_ok=True)
mesh_file = mesh_folder / "spine_mesh.h5"
mesh_tools.write_mesh(spine_mesh, mf2, mf3, mesh_file)

parent_mesh = mesh.ParentMesh(
    mesh_filename=str(mesh_file),
    mesh_filetype="hdf5",
    name="parent_mesh",
)

 2024-07-21 19:14:43,416 smart.mesh - INFO - HDF5 mesh, "parent_mesh", successfully loaded from file: spine_mesh/spine_mesh.h5! (mesh.py:245) 

 2024-07-21 19:14:43,417 smart.mesh - INFO - 0 subdomains successfully loaded from file: spine_mesh/spine_mesh.h5! (mesh.py:258) 

Initialize model and solvers.

configCur = config.Config()
configCur.solver.update(
    {
        "final_t": 5.0,
        "initial_dt": 0.05,
        "time_precision": 6,
        "use_snes": True,
    }
)

modelCur = model.Model(pc, sc, cc, rc, configCur, parent_mesh)
modelCur.initialize()

 2024-07-21 19:14:54,672 smart.model - WARNING - Warning! Initial L2-norm of compartment PM is 111.62097871138167 (possibly too large). (model.py:1190) 

 2024-07-21 19:14:55,082 smart.solvers - INFO - Jpetsc_nest assembled, size = (24802, 24802) (solvers.py:199) 

 2024-07-21 19:14:55,083 smart.solvers - INFO - Initializing block residual vector (solvers.py:207) 

 2024-07-21 19:14:55,386 smart.model_assembly - INFO - 
╒══════╤══════════════════╤═══════════════╕
│      │ Value/Equation   │ Description   │
╞══════╪══════════════════╪═══════════════╡
│ kon  │ 1.00×10⁰ 1/µM/s  │               │
├──────┼──────────────────┼───────────────┤
│ koff │ 1.00×10⁻¹ 1/s    │               │
╘══════╧══════════════════╧═══════════════╛
 (model_assembly.py:370) 

 2024-07-21 19:14:55,393 smart.model_assembly - INFO - 
╒════╤═══════════════╤═════════════════╤═══════════════════════╕
│    │ Compartment   │ D               │ Initial condition     │
╞════╪═══════════════╪═════════════════╪═══════════════════════╡
│ A  │ Cyto          │ 1.00×10⁰ µm²/s  │ 1.00×10⁰ µM           │
├────┼───────────────┼─────────────────┼───────────────────────┤
│ X  │ PM            │ 1.00×10⁻¹ µm²/s │ 1.00×10³ molecule/µm² │
├────┼───────────────┼─────────────────┼───────────────────────┤
│ B  │ PM            │ 1.00×10⁻² µm²/s │ 0.00×10⁰ molecule/µm² │
╘════╧═══════════════╧═════════════════╧═══════════════════════╛
 (model_assembly.py:370) 

 2024-07-21 19:14:56,148 smart.model_assembly - INFO - 
╒══════╤══════════════════╤═══════════╤════════════╤═════════╤════════════════╤═══════════════╕
│      │   Dimensionality │   Species │   Vertices │   Cells │   Marker value │ Size          │
╞══════╪══════════════════╪═══════════╪════════════╪═════════╪════════════════╪═══════════════╡
│ Cyto │                3 │         1 │      11562 │   48096 │              1 │ 6.71×10⁻¹ µm³ │
├──────┼──────────────────┼───────────┼────────────┼─────────┼────────────────┼───────────────┤
│ PM   │                2 │         2 │       6620 │   13107 │             10 │ 6.24×10⁰ µm²  │
╘══════╧══════════════════╧═══════════╧════════════╧═════════╧════════════════╧═══════════════╛
 (model_assembly.py:370) 

 2024-07-21 19:14:56,153 smart.model_assembly - INFO - 
╒════╤═════════════╤════════════╤════════════════╤════════════════╕
│    │ Reactants   │ Products   │ Equation       │ Type           │
╞════╪═════════════╪════════════╪════════════════╪════════════════╡
│ r1 │ ['A', 'X']  │ ['B']      │ kon*A*X-koff*B │ volume_surface │
╘════╧═════════════╧════════════╧════════════════╧════════════════╛
 (model_assembly.py:370) 

╒════╤═════════════╤══════╤══════════════════╤═════════════╤══════════════╤════════════════╕
│    │ name        │   id │   dimensionality │   num_cells │   num_facets │   num_vertices │
╞════╪═════════════╪══════╪══════════════════╪═════════════╪══════════════╪════════════════╡
│  0 │ parent_mesh │   10 │                3 │       48096 │       103186 │          11562 │
├────┼─────────────┼──────┼──────────────────┼─────────────┼──────────────┼────────────────┤
│  1 │ Cyto        │   24 │                3 │       48096 │       103186 │          11562 │
├────┼─────────────┼──────┼──────────────────┼─────────────┼──────────────┼────────────────┤
│  2 │ PM          │   31 │                2 │       13107 │        19727 │           6620 │
╘════╧═════════════╧══════╧══════════════════╧═════════════╧══════════════╧════════════════╛

Save model information to .pkl file and write initial conditions to file.

modelCur.to_pickle('modelCur.pkl')
results = dict()
result_folder = pathlib.Path("resultsSpine")
result_folder.mkdir(exist_ok=True)
for species_name, species in modelCur.sc.items:
    results[species_name] = d.XDMFFile(
        modelCur.mpi_comm_world, str(result_folder / f"{species_name}.xdmf")
    )
    results[species_name].parameters["flush_output"] = True
    results[species_name].write(modelCur.sc[species_name].u["u"], modelCur.t)

Solve the system until modelCur.t > modelCur.final_t. We display the surface distribution of species B at $t$ = 1.0 s for comparison with Figure 1 of the JOSS paper.

tvec = [0]
avg_B = [B.initial_condition]
# Set loglevel to warning in order not to pollute notebook output
logger.setLevel(logging.WARNING)
displayed = False

while True:
    # Solve the system
    modelCur.monolithic_solve()
    # Save results for post processing
    for species_name, species in modelCur.sc.items:
        results[species_name].write(modelCur.sc[species_name].u["u"], modelCur.t)
    dx = d.Measure("dx", domain=modelCur.cc['PM'].dolfin_mesh)
    int_val = d.assemble_mixed(modelCur.sc['B'].u['u']*dx)
    volume = d.assemble_mixed(1.0*dx)
    avg_B.append(int_val / volume)
    tvec.append(modelCur.t)
    if modelCur.t >= 1.0 and not displayed:
        visualization.plot(modelCur.sc["B"].u["u"], clip_logic=False, clim=(50,75))
        displayed = True
    # End if we've passed the final time
    if modelCur.t >= modelCur.final_t:
        break

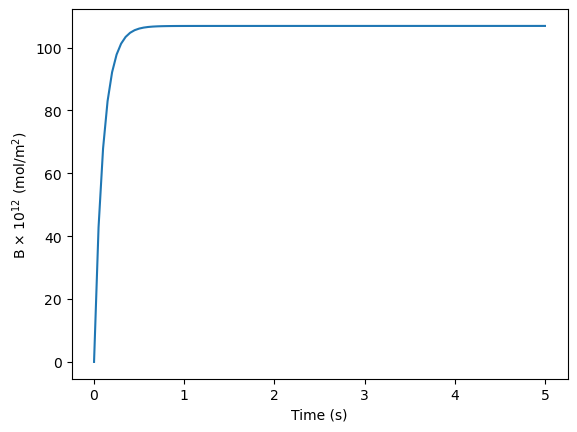
Now we plot the average concentration of B in the dendritic spine over time, which should match the plot shown in Fig 1 of JOSS.

avg_B = np.array(avg_B)
plt.plot(tvec, 1e12*avg_B*1e12/(6.02e23), label='SMART simulation')
plt.xlabel('Time (s)')
plt.ylabel('B $\\times$ $\mathrm{10^{12}~(mol/m^2)}$')

Text(0, 0.5, 'B $\\times$ $\\mathrm{10^{12}~(mol/m^2)}$')

../../_images/a1042465ad114783a03b1301de54485d7855deda2791816eaf3da24923b50866.png

Regression test against previous runs.

percent_error = 100*np.abs(avg_B[-1]-64.35444884201829)
assert percent_error < .01,\
    f"Failed regression test: Example 2-3d results deviate {percent_error:.3f}% from the previous numerical solution"