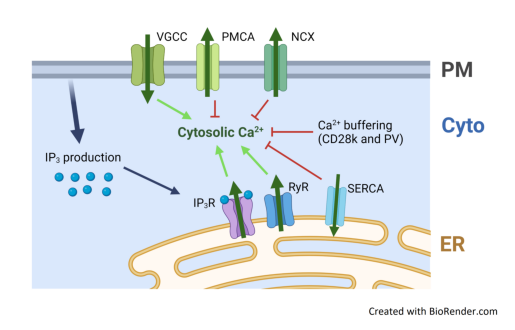
Example 6: Model for neuron calcium dynamics in 3D#
Geometry is divided into 4 domains: two volumes and two surfaces:
plasma membrane (PM) \(\Gamma_{PM}\)
Cytosol \(\Omega_{Cyto}\)
ER membrane \(\Gamma_{ERm}\)
ER lumen (ER interior) \(\Omega_{ER}\)
This model describes the response of calcium to a prescribed release of IP3 at the PM. IP3 binds to the IP3R and triggers release of calcium from the ER. Calcium also enters via a prescribed influx at the PM and also releases from the ER through ryanodine receptors (RyRs). Calcium buffering in the Cytosol (binding to CD28k or parvalbumin) is modeled explicitly via reactions, whereas buffering in the ER (primarily binding to calreticulin) is included implicitly by scaling fluxes and setting an effective diffusion coefficient for calcium. Calcium exits the cell via PMCA and NCX fluxes and is pumped back into the ER through SERCA pumps.
Overall, the distribution of species modeled are:
PM: no species, just reactions and prescribed fluxes
Cytosol: 4 species - IP3, Calcium, CD28k, and parvalbumin
ER membrane: 6 species - 3 states of RyRs and 3 states of IP3Rs
ER volume: 1 species - ER calcium (buffering is implicit)
We therefore have 11 variables to solve for, and only the volumetric species (those in the ER volume or Cytosol) have diffusive forms. The species living in the PM or ERm are effectively described by ODEs, as we neglect surface diffusion in this case.
Much of this model (excluding the RyRs) is based on the model presented in Doi et al, 2006, Journal of Neuroscience, including both parameters and equations. Other aspects of the model were developed by referring to other sources in the neuron literature. For instance, parameters were determined for the novel RyR model we use here by fitting to modeling data from Hernandez Mesa et al, 2022, PLOS Computational Biology and the equations for this model were based on those in Sobie et al, 2002, Biophysical Journal. A full description of this model will be included in an upcoming publication.
Please note that this file may take 1 hour or more to complete execution, due to the size of the model and the resolution of the mesh.
from matplotlib import pyplot as plt
import matplotlib.image as mpimg
img_A = mpimg.imread('example6-diagram.png')
plt.imshow(img_A)
plt.axis('off')
(-0.5, 2720.5, 1702.5, -0.5)
import dolfin as d
import sympy as sym
import numpy as np
import pathlib
import logging
import gmsh # must be imported before pyvista if dolfin is imported first
from smart import config, mesh, model, mesh_tools, visualization
from smart.units import unit
from smart.model_assembly import (
Compartment,
Parameter,
Reaction,
Species,
SpeciesContainer,
ParameterContainer,
CompartmentContainer,
ReactionContainer,
sbmodel_from_locals)
import petsc4py.PETSc as PETSc
from matplotlib import pyplot as plt
d.parameters["form_compiler"]["quadrature_degree"] = 4 # set quadrature degree to avoid warning from fenics
/usr/lib/python3/dist-packages/scipy/__init__.py:146: UserWarning: A NumPy version >=1.17.3 and <1.25.0 is required for this version of SciPy (detected version 1.26.4
warnings.warn(f"A NumPy version >={np_minversion} and <{np_maxversion}"
First, we define the various units for the inputs
# Aliases - base units
uM = unit.uM
um = unit.um
nm = unit.nm
molecule = unit.molecule
sec = unit.sec
dimensionless = unit.dimensionless
# Aliases - units used in model
D_unit = um**2 / sec
flux_unit = uM * um / sec
vol_unit = uM
surf_unit = molecule / um**2
and set the log level to INFO
logger = logging.getLogger("smart")
logger.setLevel(logging.INFO)
Generate model#
Define species, compartments, reactions and compartments, then store them in their respective containers.
Compartment definitions#
Define 4 compartments; specifying nonadjacency can speed up evaluation of code but is not strictly necessary.
Cyto = Compartment("Cyto", 3, um, 1)
PM = Compartment("PM", 2, um, 10)
ER = Compartment("ER", 3, um, 2)
ERm = Compartment("ERm", 2, um, 12)
PM.specify_nonadjacency(['ERm', 'ER'])
ERm.specify_nonadjacency(['PM'])
Species definitions#
Define species and diffusion coefficients in all compartments
# if we reduce the Ca diffusion coefficient, the system may diverge
Ca = Species("Ca", 0.06, vol_unit, 220.0, D_unit, "Cyto")
IP3 = Species("IP3", 0.11, vol_unit, 200.0, D_unit, "Cyto")
PV_Ca0 = 0.06*50 / (0.95/107 + 0.06) # 43.555, computed as SS conc
PV_Ca = Species('PV_Ca', PV_Ca0, uM, 43, um**2/sec, 'Cyto', 'buffer')
CD28k_hm0 = 0.06**2*100 / (0.823*(0.473+0.06)+0.06**2) # 0.814, computed as SS conc
CD28k_hm = Species('CD28k_hm', CD28k_hm0, uM, 20, um**2/sec, 'Cyto', 'buffer')
ip3r_tot = 200 # molecules/um^2
unit.define(f'ip3r_dimension = {ip3r_tot}*molecule/um**2')
ip3r_0 = Species('ip3r_0', 0.784137, unit.ip3r_dimension, 0, um**2/sec, 'ERm')
ip3r_ip3 = Species('ip3r_ip3', 0.003343, unit.ip3r_dimension, 0, um**2/sec, 'ERm')
ip3r_ip3_ca = Species('ip3r_ip3_ca', 0.000802, unit.ip3r_dimension, 0, um**2/sec, 'ERm')
ryr_x = Species('ryr_x', 0, dimensionless, 0, um**2/sec, 'ERm') # leaky integrator
ryr_y = Species('ryr_y', 0, dimensionless, 0, um**2/sec, 'ERm') # open
ryr_z = Species('ryr_z', 0, dimensionless, 0, um**2/sec, 'ERm') # refractory
CaER = Species("CaER", 150.0, vol_unit, 6.27, D_unit, "ER") # effective D due to buffering
Parameters and reaction definitions#
First, define pulse functions for use in stimulus functions.
def estep(t, t0, m): return 1 / (1+sym.exp(m*(t0-t)))
def estep_decay(t, t0, m, tau): return sym.exp((t0-t)/tau) * estep(t, t0, m)
def estep_decayI(t, t0, m, tau): return tau*(1-sym.exp((t0-t)/tau)) * estep(t, t0, m)
def astep(t, t0, m): return (1+m*(t-t0)/(1+m**2*(t-t0)**2)**(1/2))/2
def astepI(t, t0, m): return (1+m**2*(t-t0)**2)**(1/2)/(2*m) + (t-t0)/2 # Integral of astep
def astep_rect(t0, tf, m): return astep(t, t0, m) - \
astep(t, tf, m) # Rectangular pulse from t0 to tf
# Integral of rectangular pulse from t0 to tf
def astep_rectI(t0, tf, m): return astepI(t, t0, m) - astepI(t, tf, m)
def astep_str(t, t0, m): return f"(0.5+{m}/2*({t}-{t0})/(1+({m}*({t}-{t0}))**2)**0.5)"
t = sym.Symbol('t')
Define plasma membrane reactions (module a)#
a1: “simple spikes” - calcium influx at PM through VGCCs at 100 Hz
a2: “complex spike” - larger calcium influx through VGCCs at t = 0.1 s
a3: PMCA flux
a4: NCX flux
a5: calcium leak
a6: IP3 production at PM
# Ca2+ flux VGCC - simple spike from parallel fiber
# 5 pulses at 100Hz (10ms apart), each releasing 1500 ions over 1ms
# flag to change to set stimulus on (1) or off (0)
input_flag = Parameter('input_flag', 1.0, dimensionless)
zeta_psd_pm = .050*um/8 # vol/SA ratio for post-synaptic density (PSD) to PM
psd_vol = 0.5*0.5*0.05
simple_spike_flux = (1.5e6/psd_vol) * zeta_psd_pm
a1_ti = [0.01, 0.02, 0.03, 0.04, 0.05]
a1_dt = 0.001
a1_m = 20000 # rise time of <100ns both sides
a1_on_expr = simple_spike_flux * sum([astep_rect(a1_t, a1_t+a1_dt, a1_m) for a1_t in a1_ti])
a1_on_preint_expr = simple_spike_flux * \
sum([astep_rectI(a1_t, a1_t+a1_dt, a1_m) for a1_t in a1_ti])
a1_on = Parameter.from_expression('a1_on', a1_on_expr, molecule/(um**2 * sec), group='vgcc',
use_preintegration=True, preint_sym_expr=a1_on_preint_expr)
a1 = Reaction('a1', [], ['Ca'], {"k": "a1_on", 'flag': 'input_flag'},
eqn_f_str='flag*k', explicit_restriction_to_domain='PM')
# Ca2+ flux VGCC - complex spike from climbing fiber
complex_spike_flux = (2.5e6/psd_vol) * zeta_psd_pm # 5e6 molecules / (um**2 * s) [for 2 ms]
a2_t0 = 0.100
a2_tf = 0.102
a2_m = 20000 # rise time of <100ns both sides
a2_on_expr = complex_spike_flux * astep_rect(a2_t0, a2_tf, a2_m)
a2_on_preint_expr = complex_spike_flux * astep_rectI(a2_t0, a2_tf, a2_m)
a2_on = Parameter.from_expression('a2_on', a2_on_expr, molecule/(um**2 * sec), group='vgcc',
use_preintegration=True, preint_sym_expr=a2_on_preint_expr)
a2 = Reaction('a2', [], ['Ca'],
{'k': 'a2_on', 'flag': 'input_flag'}, reaction_type="prescribed", eqn_f_str='flag*k',
explicit_restriction_to_domain='PM')
# Ca2+ flux PMCA
a3_on = Parameter('a3_on', 1000, molecule/(um**2*sec))
a3_km = Parameter('a3_km', 0.1, uM)
a3 = Reaction('a3', ['Ca'], [], {"k": "a3_on", "K": "a3_km"},
explicit_restriction_to_domain='PM', eqn_f_str='k*u/(u+K)',
species_map={'u': 'Ca'})
# NCX
a4_on = Parameter('a4_on', 64000, molecule/(um**2*sec))
a4_km = Parameter('a4_km', 7.3, uM)
a4 = Reaction('a4', ['Ca'], [], {"k": "a4_on", "K": "a4_km"},
explicit_restriction_to_domain='PM', eqn_f_str='k*u**2/(u**2+K**2)',
species_map={'u': 'Ca'})
# Leak
a5_on = Parameter('a5_on', 380, molecule/(um**2*sec))
a5 = Reaction('a5', [], ['Ca'], {"k": "a5_on"},
explicit_restriction_to_domain='PM', eqn_f_str='k')
# IP3 production at the membrane
ip3_fit = (24080*800, -12.7, -24080*800, -12.8)
ip3_pulse_expr = estep(t, 0.01, 8000) * \
(ip3_fit[0]*sym.exp(ip3_fit[1]*t) + ip3_fit[2]*sym.exp(ip3_fit[3]*t))
# Not exact, but there is no indefinite integral for ip3_pulse_preint_expr.
# Since it is just a sigmoid applied to both, approximately the same
# just reduce the steepness of sigmoid
ip3_pulse_preint_expr = estep(t, 0.01, 1000) * (ip3_fit[0]/ip3_fit[1]*sym.exp(
ip3_fit[1]*t) + ip3_fit[2]/ip3_fit[3]*sym.exp(ip3_fit[3]*t) - (ip3_fit[0]/ip3_fit[1]+ip3_fit[2]/ip3_fit[3]))
a6_ip3_pulse = Parameter.from_expression('a6_ip3_pulse', ip3_pulse_expr, molecule/(um**2 * sec), group='vgcc',
use_preintegration=True, preint_sym_expr=ip3_pulse_preint_expr)
a6 = Reaction('a6', [], ['IP3'], {'k': 'a6_ip3_pulse', 'flag': 'input_flag'},
eqn_f_str='flag*k', explicit_restriction_to_domain='PM')
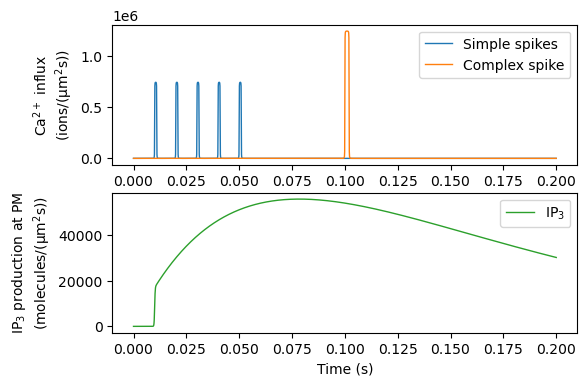
This series of reactions at the plasma membrane serves as input stimuli in the model. We can plot them over time below.
import sympy as sym
a1_func = sym.lambdify(t, a1_on_expr.magnitude, 'numpy') # pull out magnitude from pint object
a2_func = sym.lambdify(t, a2_on_expr.magnitude, 'numpy')
ip3_func = sym.lambdify(t, ip3_pulse_expr, 'numpy')
t_plot = np.linspace(0, 0.2, 2001)
fig, ax = plt.subplots(2, 1)
fig.set_size_inches(6, 4)
ax[0].plot(t_plot, a1_func(t_plot), label='Simple spikes', color='tab:blue', lw=1)
ax[0].plot(t_plot, a2_func(t_plot), label='Complex spike', color='tab:orange', lw=1)
ax[0].legend()
ax[0].set(xlabel='Time (s)',
ylabel='$\mathrm{Ca^{2+}~influx}$\n$\mathrm{(ions / (μm^2 s))}$')
ax[1].plot(t_plot, ip3_func(t_plot), label='$\mathrm{IP_3}$', color='tab:green', lw=1)
ax[1].set(xlabel='Time (s)',
ylabel='$\mathrm{IP_3~production~at~PM}$\n$\mathrm{(molecules / (μm^2 s))}$')
ax[1].legend()
<matplotlib.legend.Legend at 0x7faa2ae31ff0>
Define cytosolic reactions (module b):#
b1: Parvalbumin (PV) Ca2+ buffering
b2: calbindin-D28k (CD28k) Ca2+ buffering
b3: degradation of IP3
# Calcium buffering
b1_on = Parameter('b1_on', 107.0, 1/(uM*sec), 'ca2+ buffers', notes='PV')
b1_off = Parameter('b1_off', 0.95, 1/sec, 'ca2+ buffers', notes='PV')
PVtot = Parameter('PVtot', 50, uM, 'ca2+ buffers')
b2_on = Parameter('b2_on', 5.5, 1/(uM*sec), 'ca2+ buffers', notes='cd28k_high')
b2_Kdh = Parameter('b2_Kdh', 0.473, uM, 'ca2+ buffers', notes='cd28k_high')
b2_Kdm = Parameter('b2_Kdm', 0.823, uM, 'ca2+ buffers', notes='cd28k_med')
CD28ktot = Parameter('CD28ktot', 100, uM, 'ca2+ buffers')
b1 = Reaction('b1', ['Ca'], ['PV_Ca'],
{'kf': 'b1_on', 'kr': 'b1_off', 'btot': 'PVtot'},
species_map={'u': 'Ca', 'b': 'PV_Ca'},
eqn_f_str='kf*u*(btot-b) - kr*b')
b2 = Reaction('b2', ['Ca', 'Ca'], ['CD28k_hm'],
{'b2_on': 'b2_on', 'b2_Kdh': 'b2_Kdh', 'b2_Kdm': 'b2_Kdm', 'btot': 'CD28ktot'},
species_map={'u': 'Ca', 'b': 'CD28k_hm'},
eqn_f_str='b2_on*(u*(btot-b) - b2_Kdm*b*(1+b2_Kdh/u))')
# degradation of IP3
b3_on = Parameter('b3_on', 0.14, 1/sec, 'ip3 production')
b3_ip3basal = Parameter('b3_ip3basal', 0.11, uM)
b3 = Reaction('b3', ['IP3'], [], {"k": "b3_on", 'u0': 'b3_ip3basal'},
eqn_f_str='k*(u-u0)', species_map={'u': 'IP3'},)
Define ER membrane reactions (module c).#
These reactions are effectively ODEs, as we do not allow RyRs or IP3Rs in the ER membrane to diffuse.
The IP3Rs can be in 1 of 4 states (given as their variable names here). We define them each normalized to the total receptor concentration, such that they are by definition between 0 and 1.
ip3r0: free, unbound receptor (closed)ip3r_ip3: receptors with only IP3 bound (transition state, closed)ip3r_ip3_ca: receptors with IP3 and Ca2+ bound (OPEN)ip3r_ca: receptors with only Ca2+ bound (deactivated, closed) If we assume that the total number of receptors is conserved, we only need to define 3 species of IP3R, as we do below. The 4th,ip3r_ca, can be calculated as1 - ip3r0 - ip3r_ip3 - ip3r_ip3_ca.
The IP3R reactions are as follows:
c1_1: ip3 + ip3r0 <-> ip3r_ip3
c1_2: ca + ip3r_ip3 <-> ip3r_ip3_ca
c1_3: ca + ip3r0 <-> ip3r_0
and the resultant calcium flux is given as:
c1: c1_on * ip3r_ip3_ca * (CaER - Ca)
# Multi-state IP3R model
c1_on_1 = Parameter('c1_on_1', 1000, 1/(uM*sec), 'ip3r_multistate')
c1_off_1 = Parameter('c1_off_1', 25800, 1/sec, 'ip3r_multistate')
c1_on_2 = Parameter('c1_on_2', 8000, 1/(uM*sec), 'ip3r_multistate')
c1_off_2 = Parameter('c1_off_2', 2000, 1/sec, 'ip3r_multistate')
c1_on_3 = Parameter('c1_on_3', 9, 1/(uM*sec), 'ip3r_multistate')
c1_off_3 = Parameter('c1_off_3', 2, 1/sec, 'ip3r_multistate')
ip3r_tot_param = Parameter('ip3r_tot_param', 1, unit.ip3r_dimension, 'ip3r_multistate')
c1_1 = Reaction('c1_1', ['ip3r_0', 'IP3'], ['ip3r_ip3'], {
"on": "c1_on_1", "off": "c1_off_1"}, group='ip3r_multistate')
c1_2 = Reaction('c1_2', ['ip3r_ip3', 'Ca'], ['ip3r_ip3_ca'], {
"on": "c1_on_2", "off": "c1_off_2"}, group='ip3r_multistate')
c1_3 = Reaction('c1_3', ['ip3r_0', 'Ca'], [], {'kf': 'c1_on_3', 'kr': 'c1_off_3', 'ip3r_tot': 'ip3r_tot_param'},
eqn_f_str='kf*ip3r_0*Ca - kr*(ip3r_tot-ip3r_0-ip3r_ip3-ip3r_ip3_ca)',
species_map={'ip3r_0': 'ip3r_0', 'ip3r_ip3': 'ip3r_ip3', 'ip3r_ip3_ca': 'ip3r_ip3_ca', 'Ca': 'Ca'}, group='ip3r_multistate')
c1_on = Parameter('c1_on', 30, 1/(uM*sec), 'ip3r_multistate')
c1 = Reaction('c1', ['CaER'], ['Ca'],
{"k": "c1_on"}, eqn_f_str='k*R*(uER-u)',
explicit_restriction_to_domain='ERm', species_map={'R': 'ip3r_ip3_ca', 'u': 'Ca', 'uER': 'CaER'})
The RyRs can be in 1 of 4 states (given as their variable names here). We define them each normalized to the total receptor concentration, such that they are by definition between 0 and 1.
ryr_w: closed channelsryr_x: “leaky integrator” state (still closed)ryr_y: open channelsryr_z: “refractory” state If we assume that the total number of receptors is conserved, we only need to define 3 species of RyR, as we do below. The 4th,ryr_w, can be calculated as1 - ryr_x - ryr_y - ryr_z.
Unlike for the IP3Rs, RyR reactions are not given by simple mass action relations. The main equations for the transitions between receptor states are given by:
c2_fxy: ryr_x (x) -> ryr_y (y), forward reaction rate:
\[k_{c2,xy} x\]
c2_fyz: ryr_y (y) -> ryr_z (z), forward reaction rate:
\[k_{c2,yz} y \frac{1 + \gamma_3 z^3}{z^3 + \gamma_4^3}\]
c2_fzw: ryr_z (z) -> ryr_w (w), forward reaction rate:
\[k_{c2,zw} z \sigma[yxT, y+x, m2]\]
c2_fwx: ryr_w (w) -> ryr_x (x), forward reaction rate:
\[k_{c2,wx} (1-x-y-z) \frac{c^4}{c^4 + (\gamma_1-\gamma_2 c_{ER})^4} \sigma[c, c_{min}, m]\]
where \(\sigma[x, x_{min}, m]\) defines a steep sigmoidal function, which acts as a continuous approximation of a Heaviside function, such that the function is close to 1 when \(x > x_{min}\) and is close to 0 when \(x < x_{min}\). In this case, the function approaches a Heaviside function as \(m \rightarrow \infty\). In the expression of c2_fwx, \(c\) denotes Ca and \(c_{ER}\) denotes CaER
The resultant calcium flux is given as:
c2: c2_on * ryr_y * (CaER - Ca)
# Custom RyR Model (with inactivation + refractory period)
# States:
# w = Closed, x = leaky integrator, y = open, z = refractory
c2_kwx = Parameter('c2_kwx', 100, 1/sec, 'ryr') # closed -> leaky integrator
c2_kxy = Parameter('c2_kxy', 500, 1/sec, 'ryr') # leaky integrator -> open
c2_kyz = Parameter('c2_kyz', 125, 1/sec, 'ryr') # open -> refractory
c2_kzw = Parameter('c2_kzw', 125/10, 1/sec, 'ryr') # refractory -> closed
c2_g1 = Parameter('c2_g1', 6, uM, 'ryr')
c2_g2 = Parameter('c2_g2', 0.032, dimensionless, 'ryr')
c2_g3 = Parameter('c2_g3', 30, dimensionless, 'ryr')
c2_g4 = Parameter('c2_g4', 0.6, dimensionless, 'ryr')
c2_cmin = Parameter('c2_cmin', 1.5, uM, 'ryr')
c2_m = Parameter('c2_m', 10, 1/uM, 'ryr')
c2_yxT = Parameter('c2_yxT', 0.0001, dimensionless, 'ryr')
c2_m2 = Parameter('c2_m2', 1e6, dimensionless, 'ryr')
c2_fxy = Reaction('c2_fxy', ['ryr_x'], ['ryr_y'], {"k": "c2_kxy"},
species_map={'x': 'ryr_x'}, eqn_f_str=f"k*x")
c2_fyz = Reaction('c2_fyz', ['ryr_y'], ['ryr_z'], {"k": "c2_kyz", "g3": "c2_g3", "g4": "c2_g4"},
species_map={'y': 'ryr_y', 'z': 'ryr_z'}, eqn_f_str=f"k*y*(1+g3*z**3/(z**3+g4**3))")
# Accounting for conservation of mass, w (closed channels) is 1-x-y-z
c2_fwx = Reaction('c2_fwx', [], ['ryr_x'], {"k": "c2_kwx", "g1": "c2_g1", "m": "c2_m", "g2": "c2_g2", "cmin": "c2_cmin"},
species_map={'c': 'Ca', 'cer': 'CaER',
'x': 'ryr_x', 'y': 'ryr_y', 'z': 'ryr_z'},
eqn_f_str=f"k*(1-x-y-z)*c**4/(c**4+(g1-g2*cer)**4)*{astep_str('c','cmin','m')}")
c2_fzw = Reaction('c2_fzw', ['ryr_z'], [], {"k": "c2_kzw", "yxT": "c2_yxT", "m2": "c2_m2"},
species_map={'x': 'ryr_x', 'y': 'ryr_y', 'z': 'ryr_z'}, eqn_f_str=f"k*z*{astep_str('yxT','(y+x)','m2')}")
c2_ryr_kf = Parameter('c2_ryr_kf', 25000, molecule/(uM*um**2*sec), 'ryr')
c2 = Reaction('c2', ['CaER'], ['Ca'], {'k': 'c2_ryr_kf'},
species_map={'c': 'Ca', 'cer': 'CaER', 'y': 'ryr_y'},
eqn_f_str='k*(cer-c)*y', explicit_restriction_to_domain='ERm')
Now we define the remaining fluxes at the ER membrane:
c3: Sarco-endoplasmic reticulum calcium ATPase (SERCA) pumping cytosolic Ca2+ into the ER
c4: Ca2+ leak out of the ER (computed from SS considerations)
# SERCA
c3_f = Parameter('c3_f', 18000,
molecule/(um**2*sec), 'serca')
c3_m = Parameter('c3_m', 0.27, uM, 'serca')
c3 = Reaction('c3', ['Ca'], ['CaER'],
{"k": "c3_f", "K": "c3_m"}, eqn_f_str='k*u**2/(u**2+K**2)',
explicit_restriction_to_domain='ERm', species_map={'u': 'Ca', 'CaER': 'CaER'})
# Leak from ER
ca_ss = 0.06*uM
# leak = serca(t=0) - ip3r(t=0) - ryr(t=0) [ryr(t=0)==0]
serca_ss = c3_f.quantity * ca_ss**2/(ca_ss**2+c3_m.quantity**2)
ip3r_ip3_ca_ss = ip3r_tot*0.000802*molecule/um**2
ip3r_ss = ip3r_ip3_ca_ss * c1_on.quantity * (150-0.06)*uM
c4_on_quantity = (serca_ss - ip3r_ss)/((150-0.06)*uM) # molecule/(um**2*uM*sec)
assert c4_on_quantity.magnitude > 0
assert c4_on_quantity.units == molecule/(um**2*uM*sec)
c4_on = Parameter('c4_on', c4_on_quantity.magnitude, c4_on_quantity.units, 'leak')
c4 = Reaction('c4', ['CaER'], ['Ca'], {"k": "c4_on"},
eqn_f_str='k*(uER-u)',
species_map={'u': 'Ca', 'uER': 'CaER'},
explicit_restriction_to_domain='ERm')
Now we scale the fluxes in and out of the ER to implictly account for calcium buffering in the ER. In this case, we assume that \(1-\xi\) fraction of Ca2+ ions are immediately buffered upon entering the ER, and, conversely, \(1-\xi\) fraction of a flux out of the ER comes from ions released by calcium buffers.
xi = 0.0227272727
for c in [c1, c2, c3, c4]:
c.flux_scaling = {'CaER': xi}
c.__post_init__()
Finally, we gather all parameters, species, compartments and reactions in containers. The function sbmodel_from_locals looks for all local variables that are either parameter, species, compartment, or reaction objects and adds them to separate containers.
pc, sc, cc, rc = sbmodel_from_locals(locals().values())
Define mesh, model, and solver#
Define mesh as a sphere-in-a-sphere and view using pyvista.
# only equivalent to a portion of the cell (total size would be on the order of 10 microns)
curRadius = 2
ERFrac = 0.5 # how wide the ER is relative to the entire volume here
# =============================================================================================
# Create/load in mesh
# =============================================================================================
# Base mesh
domain, facet_markers, cell_markers = mesh_tools.create_spheres(
curRadius, curRadius*ERFrac, hEdge=0.2, hInnerEdge=0.2)
# Write mesh and meshfunctions to file
mesh_folder = pathlib.Path("mesh")
mesh_folder.mkdir(exist_ok=True)
mesh_path = mesh_folder / "DemoSphere.h5"
mesh_tools.write_mesh(domain, facet_markers, cell_markers, filename=mesh_path)
parent_mesh = mesh.ParentMesh(
mesh_filename=str(mesh_path),
mesh_filetype="hdf5",
name="parent_mesh",
)
visualization.plot_dolfin_mesh(domain, cell_markers, facet_markers, outer_marker=10)
2024-05-07 13:05:19,328 smart.mesh - INFO - HDF5 mesh, "parent_mesh", successfully loaded from file: mesh/DemoSphere.h5! (mesh.py:245)
2024-05-07 13:05:19,329 smart.mesh - INFO - 0 subdomains successfully loaded from file: mesh/DemoSphere.h5! (mesh.py:258)
Initialize solver and model.
config_cur = config.Config()
model_cur = model.Model(pc, sc, cc, rc, config_cur, parent_mesh)
DT_INITIAL = .002
DT_SMALL = 0.0001
SIMPLE_SPIKES = [0.01, 0.02, 0.03, 0.04, 0.05]
COMPLEX_SPIKES = [0.1]
adjust_dt = list()
for t in SIMPLE_SPIKES:
adjust_dt.extend([(round(t-40*DT_SMALL, 4), 4*DT_SMALL)])
adjust_dt.extend([(round(t-12*DT_SMALL, 4), 2*DT_SMALL)])
adjust_dt.extend([(round(t-4*DT_SMALL, 4), DT_SMALL)])
for t in COMPLEX_SPIKES:
adjust_dt.extend([(round(t-40*DT_SMALL, 4), 4*DT_SMALL)])
adjust_dt.extend([(round(t-12*DT_SMALL, 4), 2*DT_SMALL)])
adjust_dt.extend([(round(t-4*DT_SMALL, 4), DT_SMALL)])
config_cur.solver.update(
{
"final_t": 0.2,
"initial_dt": DT_INITIAL,
"adjust_dt": adjust_dt,
"time_precision": 6,
}
)
model_cur.initialize()
# can scale terms associated with certain compartments in the variational form
# here, this scaling was found to help with numerical stability
model_cur.set_form_scaling('cyto', 0.01, False)
# most of these were originally set in smart.model and altered here to tailor this problem
if config_cur.solver['use_snes']:
model_cur.solver.setType('newtonls')
model_cur.solver.setTolerances(rtol=1e-4)
opts = PETSc.Options()
opts['snes_linesearch_type'] = 'basic'
model_cur.solver.setFromOptions()
# set number of failed solves (tailored to this problem)
model_cur.solver.setMaxKSPFailures(200)
model_cur.solver.setMaxLinearSolveFailures(200)
# relax solver tolerances (tailored to this problem)
rtol_scale = 1.5
atol_scale = 1
model_cur.solver.setTolerances(1e-6*rtol_scale, 1e-6*atol_scale, 1e-20, 50)
ksp_rtol_scale = 1.5
ksp_atol_scale = 1
ksp_maxits = 1e5 # default 1e4
model_cur.solver.ksp.setTolerances(1e-4*ksp_rtol_scale, 1e-6*ksp_atol_scale, 1e6, ksp_maxits)
2024-05-07 13:05:46,999 smart.solvers - INFO - Jpetsc_nest assembled, size = (18781, 18781) (solvers.py:199)
2024-05-07 13:05:47,000 smart.solvers - INFO - Initializing block residual vector (solvers.py:207)
2024-05-07 13:05:47,566 smart.model_assembly - INFO -
╒════════════════╤═════════════════════════════╤═════════════════════╤═══════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╤════════════╤═════════════════╕
│ │ quantity │ is_time_dependent │ sym_expr │ notes │ group │
╞════════════════╪═════════════════════════════╪═════════════════════╪═══════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╪════════════╪═════════════════╡
│ input_flag │ 1.00×10⁰ │ False │ │ │ │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ a1_on │ 9.77×10⁻¹ molecule/s/µm² │ True │ -375000.0*(20000*t - 1020.0)/(400000000*(t - 0.051)**2 + 1)**0.5 + 375000.0*(20000*t - 1000.0)/(400000000*(t - 0.05)**2 + 1)**0.5 - 375000.0*(20000*t - 820.0)/(400000000*(t - 0.041)**2 + 1)**0.5 + 375000.0*(20000*t - 800.0)/(400000000*(t - 0.04)**2 + 1)**0.5 - 375000.0*(20000*t - 620.0)/(400000000*(t - 0.031)**2 + 1)**0.5 + 375000.0*(20000*t - 600.0)/(400000000*(t - 0.03)**2 + 1)**0.5 - 375000.0*(20000*t - 420.0)/(400000000*(t - 0.021)**2 + 1)**0.5 + 375000.0*(20000*t - 400.0)/(400000000*(t - 0.02)**2 + 1)**0.5 - 375000.0*(20000*t - 220.0)/(400000000*(t - 0.011)**2 + 1)**0.5 + 375000.0*(20000*t - 200.0)/(400000000*(t - 0.01)**2 + 1)**0.5 │ │ vgcc │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ a2_on │ 3.03×10⁻³ molecule/s/µm² │ True │ -625000.0*(20000*t - 2040.0)/(400000000*(t - 0.102)**2 + 1)**0.5 + 625000.0*(20000*t - 2000.0)/(400000000*(t - 0.1)**2 + 1)**0.5 │ │ vgcc │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ a3_on │ 1.00×10³ molecule/s/µm² │ False │ │ │ │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ a3_km │ 1.00×10⁻¹ µM │ False │ │ │ │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ a4_on │ 6.40×10⁴ molecule/s/µm² │ False │ │ │ │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ a4_km │ 7.30×10⁰ µM │ False │ │ │ │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ a5_on │ 3.80×10² molecule/s/µm² │ False │ │ │ │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ a6_ip3_pulse │ 0.00×10⁰ molecule/s/µm² │ True │ (-19264000*exp(-12.8*t) + 19264000*exp(-12.7*t))/(1 + 5.54062238439351e+34*exp(-8000*t)) │ │ vgcc │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ b1_on │ 1.07×10² 1/s/µM │ False │ │ PV │ ca2+ buffers │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ b1_off │ 9.50×10⁻¹ 1/s │ False │ │ PV │ ca2+ buffers │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ PVtot │ 5.00×10¹ µM │ False │ │ │ ca2+ buffers │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ b2_on │ 5.50×10⁰ 1/s/µM │ False │ │ cd28k_high │ ca2+ buffers │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ b2_Kdh │ 4.73×10⁻¹ µM │ False │ │ cd28k_high │ ca2+ buffers │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ b2_Kdm │ 8.23×10⁻¹ µM │ False │ │ cd28k_med │ ca2+ buffers │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ CD28ktot │ 1.00×10² µM │ False │ │ │ ca2+ buffers │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ b3_on │ 1.40×10⁻¹ 1/s │ False │ │ │ ip3 production │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ b3_ip3basal │ 1.10×10⁻¹ µM │ False │ │ │ │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c1_on_1 │ 1.00×10³ 1/s/µM │ False │ │ │ ip3r_multistate │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c1_off_1 │ 2.58×10⁴ 1/s │ False │ │ │ ip3r_multistate │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c1_on_2 │ 8.00×10³ 1/s/µM │ False │ │ │ ip3r_multistate │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c1_off_2 │ 2.00×10³ 1/s │ False │ │ │ ip3r_multistate │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c1_on_3 │ 9.00×10⁰ 1/s/µM │ False │ │ │ ip3r_multistate │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c1_off_3 │ 2.00×10⁰ 1/s │ False │ │ │ ip3r_multistate │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ ip3r_tot_param │ 1.00×10⁰ ip3r_dimension │ False │ │ │ ip3r_multistate │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c1_on │ 3.00×10¹ 1/s/µM │ False │ │ │ ip3r_multistate │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c2_kwx │ 1.00×10² 1/s │ False │ │ │ ryr │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c2_kxy │ 5.00×10² 1/s │ False │ │ │ ryr │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c2_kyz │ 1.25×10² 1/s │ False │ │ │ ryr │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c2_kzw │ 1.25×10¹ 1/s │ False │ │ │ ryr │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c2_g1 │ 6.00×10⁰ µM │ False │ │ │ ryr │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c2_g2 │ 3.20×10⁻² │ False │ │ │ ryr │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c2_g3 │ 3.00×10¹ │ False │ │ │ ryr │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c2_g4 │ 6.00×10⁻¹ │ False │ │ │ ryr │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c2_cmin │ 1.50×10⁰ µM │ False │ │ │ ryr │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c2_m │ 1.00×10¹ 1/µM │ False │ │ │ ryr │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c2_yxT │ 1.00×10⁻⁴ │ False │ │ │ ryr │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c2_m2 │ 1.00×10⁶ │ False │ │ │ ryr │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c2_ryr_kf │ 2.50×10⁴ molecule/s/µM/µm² │ False │ │ │ ryr │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c3_f │ 1.80×10⁴ molecule/s/µm² │ False │ │ │ serca │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c3_m │ 2.70×10⁻¹ µM │ False │ │ │ serca │
├────────────────┼─────────────────────────────┼─────────────────────┼───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┼────────────┼─────────────────┤
│ c4_on │ 8.37×10⁻¹ molecule/s/µM/µm² │ False │ │ │ leak │
╘════════════════╧═════════════════════════════╧═════════════════════╧═══════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╧════════════╧═════════════════╛
(model_assembly.py:337)
2024-05-07 13:05:47,577 smart.model_assembly - INFO -
╒═════════════╤════════════════════╤════════════════╤═════════════════════╤═════════════════════════╕
│ │ compartment_name │ Diffusion │ initial_condition │ concentration_units │
╞═════════════╪════════════════════╪════════════════╪═════════════════════╪═════════════════════════╡
│ Ca │ Cyto │ 2.20×10² µm²/s │ 0.06 │ 1.00×10⁰ µM │
├─────────────┼────────────────────┼────────────────┼─────────────────────┼─────────────────────────┤
│ IP3 │ Cyto │ 2.00×10² µm²/s │ 0.11 │ 1.00×10⁰ µM │
├─────────────┼────────────────────┼────────────────┼─────────────────────┼─────────────────────────┤
│ PV_Ca │ Cyto │ 4.30×10¹ µm²/s │ 43.555 │ 1.00×10⁰ µM │
├─────────────┼────────────────────┼────────────────┼─────────────────────┼─────────────────────────┤
│ CD28k_hm │ Cyto │ 2.00×10¹ µm²/s │ 0.814003 │ 1.00×10⁰ µM │
├─────────────┼────────────────────┼────────────────┼─────────────────────┼─────────────────────────┤
│ ip3r_0 │ ERm │ 0.00×10⁰ µm²/s │ 0.784137 │ 1.00×10⁰ ip3r_dimension │
├─────────────┼────────────────────┼────────────────┼─────────────────────┼─────────────────────────┤
│ ip3r_ip3 │ ERm │ 0.00×10⁰ µm²/s │ 0.003343 │ 1.00×10⁰ ip3r_dimension │
├─────────────┼────────────────────┼────────────────┼─────────────────────┼─────────────────────────┤
│ ip3r_ip3_ca │ ERm │ 0.00×10⁰ µm²/s │ 0.000802 │ 1.00×10⁰ ip3r_dimension │
├─────────────┼────────────────────┼────────────────┼─────────────────────┼─────────────────────────┤
│ ryr_x │ ERm │ 0.00×10⁰ µm²/s │ 0 │ 1.00×10⁰ │
├─────────────┼────────────────────┼────────────────┼─────────────────────┼─────────────────────────┤
│ ryr_y │ ERm │ 0.00×10⁰ µm²/s │ 0 │ 1.00×10⁰ │
├─────────────┼────────────────────┼────────────────┼─────────────────────┼─────────────────────────┤
│ ryr_z │ ERm │ 0.00×10⁰ µm²/s │ 0 │ 1.00×10⁰ │
├─────────────┼────────────────────┼────────────────┼─────────────────────┼─────────────────────────┤
│ CaER │ ER │ 6.27×10⁰ µm²/s │ 150 │ 1.00×10⁰ µM │
╘═════════════╧════════════════════╧════════════════╧═════════════════════╧═════════════════════════╛
(model_assembly.py:337)
2024-05-07 13:05:48,322 smart.model_assembly - INFO -
╒══════╤══════════════════╤═══════════════╤════════════════╤════════════╤═════════════╤═══════════════╤══════════════╕
│ │ dimensionality │ num_species │ num_vertices │ num_dofs │ num_cells │ cell_marker │ nvolume │
╞══════╪══════════════════╪═══════════════╪════════════════╪════════════╪═════════════╪═══════════════╪══════════════╡
│ Cyto │ 3 │ 4 │ 3886 │ 15544 │ 17696 │ 1 │ 2.93×10¹ µm³ │
├──────┼──────────────────┼───────────────┼────────────────┼────────────┼─────────────┼───────────────┼──────────────┤
│ PM │ 2 │ 0 │ 1642 │ 0 │ 3280 │ 10 │ 5.02×10¹ µm² │
├──────┼──────────────────┼───────────────┼────────────────┼────────────┼─────────────┼───────────────┼──────────────┤
│ ER │ 3 │ 1 │ 663 │ 663 │ 2633 │ 2 │ 4.13×10⁰ µm³ │
├──────┼──────────────────┼───────────────┼────────────────┼────────────┼─────────────┼───────────────┼──────────────┤
│ ERm │ 2 │ 6 │ 429 │ 2574 │ 854 │ 12 │ 1.25×10¹ µm² │
╘══════╧══════════════════╧═══════════════╧════════════════╧════════════╧═════════════╧═══════════════╧══════════════╛
(model_assembly.py:337)
2024-05-07 13:05:48,340 smart.model_assembly - INFO -
╒════════╤════════════════════╤═════════════════╤════════════════════════════════════════════════════╤══════════════════════╕
│ │ lhs │ rhs │ eqn_f_str │ eqn_r_str │
╞════════╪════════════════════╪═════════════════╪════════════════════════════════════════════════════╪══════════════════════╡
│ a1 │ [] │ ['Ca'] │ a1_on*input_flag │ │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ a2 │ [] │ ['Ca'] │ a2_on*input_flag │ │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ a3 │ ['Ca'] │ [] │ Ca*a3_on/(Ca + a3_km) │ │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ a4 │ ['Ca'] │ [] │ Ca**2*a4_on/(Ca**2 + a4_km**2) │ │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ a5 │ [] │ ['Ca'] │ a5_on │ │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ a6 │ [] │ ['IP3'] │ a6_ip3_pulse*input_flag │ │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ b1 │ ['Ca'] │ ['PV_Ca'] │ Ca*b1_on*(-PV_Ca + PVtot) - PV_Ca*b1_off │ │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ b2 │ ['Ca', 'Ca'] │ ['CD28k_hm'] │ b2_on*(-CD28k_hm*b2_Kdm*(1 + b2_Kdh/Ca) + │ │
│ │ │ │ Ca*(-CD28k_hm + CD28ktot)) │ │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ b3 │ ['IP3'] │ [] │ b3_on*(IP3 - b3_ip3basal) │ │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ c1_1 │ ['ip3r_0', 'IP3'] │ ['ip3r_ip3'] │ c1_on_1*ip3r_0*IP3 │ c1_off_1*ip3r_ip3 │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ c1_2 │ ['ip3r_ip3', 'Ca'] │ ['ip3r_ip3_ca'] │ c1_on_2*ip3r_ip3*Ca │ c1_off_2*ip3r_ip3_ca │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ c1_3 │ ['ip3r_0', 'Ca'] │ [] │ Ca*c1_on_3*ip3r_0 - c1_off_3*(-ip3r_0 - ip3r_ip3 - │ │
│ │ │ │ ip3r_ip3_ca + ip3r_tot_param) │ │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ c1 │ ['CaER'] │ ['Ca'] │ c1_on*ip3r_ip3_ca*(-Ca + CaER) │ │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ c2_fxy │ ['ryr_x'] │ ['ryr_y'] │ c2_kxy*ryr_x │ │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ c2_fyz │ ['ryr_y'] │ ['ryr_z'] │ c2_kyz*ryr_y*(c2_g3*ryr_z**3/(c2_g4**3 + ryr_z**3) │ │
│ │ │ │ + 1) │ │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ c2_fwx │ [] │ ['ryr_x'] │ Ca**4*c2_kwx*(c2_m*(Ca - c2_cmin)/(2*(c2_m**2*(Ca │ │
│ │ │ │ - c2_cmin)**2 + 1)**0.5) + 0.5)*(-ryr_x - ryr_y - │ │
│ │ │ │ ryr_z + 1)/(Ca**4 + (-CaER*c2_g2 + c2_g1)**4) │ │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ c2_fzw │ ['ryr_z'] │ [] │ c2_kzw*ryr_z*(c2_m2*(c2_yxT - ryr_x - │ │
│ │ │ │ ryr_y)/(2*(c2_m2**2*(c2_yxT - ryr_x - ryr_y)**2 + │ │
│ │ │ │ 1)**0.5) + 0.5) │ │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ c2 │ ['CaER'] │ ['Ca'] │ c2_ryr_kf*ryr_y*(-Ca + CaER) │ │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ c3 │ ['Ca'] │ ['CaER'] │ Ca**2*c3_f/(Ca**2 + c3_m**2) │ │
├────────┼────────────────────┼─────────────────┼────────────────────────────────────────────────────┼──────────────────────┤
│ c4 │ ['CaER'] │ ['Ca'] │ c4_on*(-Ca + CaER) │ │
╘════════╧════════════════════╧═════════════════╧════════════════════════════════════════════════════╧══════════════════════╛
(model_assembly.py:337)
╒════╤═════════════╤══════╤══════════════════╤═════════════╤══════════════╤════════════════╕
│ │ name │ id │ dimensionality │ num_cells │ num_facets │ num_vertices │
╞════╪═════════════╪══════╪══════════════════╪═════════════╪══════════════╪════════════════╡
│ 0 │ parent_mesh │ 16 │ 3 │ 20329 │ 42298 │ 4120 │
├────┼─────────────┼──────┼──────────────────┼─────────────┼──────────────┼────────────────┤
│ 1 │ Cyto │ 40 │ 3 │ 17696 │ 37459 │ 3886 │
├────┼─────────────┼──────┼──────────────────┼─────────────┼──────────────┼────────────────┤
│ 2 │ PM │ 47 │ 2 │ 3280 │ 4920 │ 1642 │
├────┼─────────────┼──────┼──────────────────┼─────────────┼──────────────┼────────────────┤
│ 3 │ ER │ 53 │ 3 │ 2633 │ 5693 │ 663 │
├────┼─────────────┼──────┼──────────────────┼─────────────┼──────────────┼────────────────┤
│ 4 │ ERm │ 60 │ 2 │ 854 │ 1281 │ 429 │
╘════╧═════════════╧══════╧══════════════════╧═════════════╧══════════════╧════════════════╛
Solve system#
Save model information in a .pkl file, then initialize saving directory and results files and simulate until model_cur.t > model_cur.final_t. Display calcium in cytosol when t ~ 0.111 s.
model_cur.to_pickle("model_cur.pkl")
# Write initial condition(s) to file
results = dict()
result_folder = pathlib.Path(f"results")
result_folder.mkdir(exist_ok=True)
for species_name, species in model_cur.sc.items:
results[species_name] = d.XDMFFile(
model_cur.mpi_comm_world, str(result_folder / f"{species_name}.xdmf")
)
results[species_name].parameters["flush_output"] = True
results[species_name].write(model_cur.sc[species_name].u["u"], model_cur.t)
# define integration measures and initialize data storage arrays
dx_Cyto = d.Measure("dx", domain=model_cur.cc['Cyto'].dolfin_mesh)
volume_Cyto = d.assemble_mixed(1.0*dx_Cyto)
cytoCaVec = np.array([Ca.initial_condition])
dx_ER = d.Measure("dx", domain=model_cur.cc['ER'].dolfin_mesh)
volume_ER = d.assemble_mixed(1.0*dx_ER)
ERCaVec = np.array([CaER.initial_condition])
# Set loglevel to warning in order not to pollute notebook output
logger.setLevel(logging.WARNING)
# Solve
displayed = False
while True:
# Solve the system
model_cur.monolithic_solve()
model_cur.adjust_dt()
# Save results for post processing
for species_name, species in model_cur.sc.items:
results[species_name].write(model_cur.sc[species_name].u["u"], model_cur.t)
# integrate
int_val_Cyto = d.assemble_mixed(model_cur.sc['Ca'].u['u']*dx_Cyto)
cytoCaCur = np.array([int_val_Cyto / volume_Cyto])
cytoCaVec = np.concatenate((cytoCaVec, cytoCaCur))
int_val_ER = d.assemble_mixed(model_cur.sc['CaER'].u['u']*dx_ER)
ERCaCur = np.array([int_val_ER / volume_ER])
ERCaVec = np.concatenate((ERCaVec, ERCaCur))
# save current time to txt file
np.savetxt(result_folder / f"tvec.txt", np.array(model_cur.tvec).astype(np.float32))
# display at t~0.111 s
if model_cur.t >= 0.111 and not displayed:
visualization.plot(model_cur.sc['Ca'].u['u'])
displayed = True
# End if we've passed the final time
if model_cur.t >= model_cur.final_t:
break
Plot calcium concentration in the cytosol over time and calcium concentration in the ER over time.
fig, ax = plt.subplots(2, 1)
fig.set_size_inches(6, 6.5)
ax[0].plot(model_cur.tvec, cytoCaVec, color='b', lw=1)
ax[0].set(xlabel='Time (s)',
ylabel='Cytosolic calcium (μM)')
ax[1].plot(model_cur.tvec, ERCaVec, color='tab:brown', lw=1)
ax[1].set(xlabel='Time (s)',
ylabel='ER calcium (μM)')
[Text(0.5, 0, 'Time (s)'), Text(0, 0.5, 'ER calcium (μM)')]
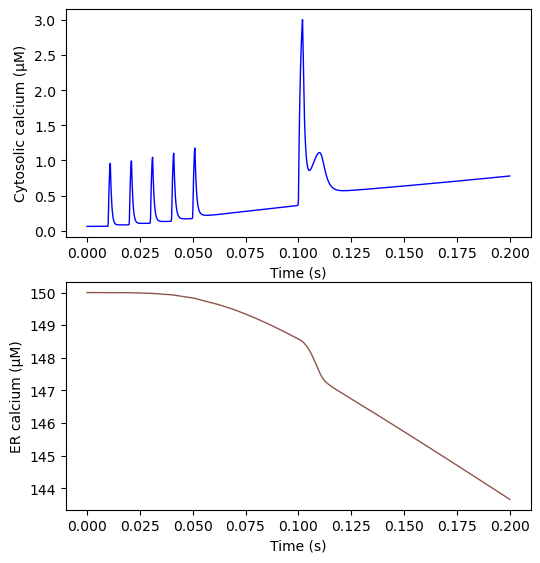
Compare ER calcium and cytosolic calcium area-under-the-curve for this simulation vs. previous runs (regression test).
tvec = np.zeros(len(model_cur.tvec))
for i in range(len(model_cur.tvec)):
tvec[i] = float(model_cur.tvec[i])
ca_cyto_auc = np.trapz(cytoCaVec, tvec)
ca_er_auc = np.trapz(ERCaVec, tvec)
ca_cyto_auc_stored = 0.09937979171915279
ca_er_auc_stored = 29.541870200036573
auc_list = [np.abs(ca_cyto_auc - ca_cyto_auc_stored)/ca_cyto_auc_stored,
np.abs(ca_er_auc - ca_er_auc_stored)/ca_er_auc_stored]
assert max(auc_list) < .01/100,\
f"Failed regression test: Example 6 results deviate {max(auc_list)*100:.3f}% from the previous numerical solution"